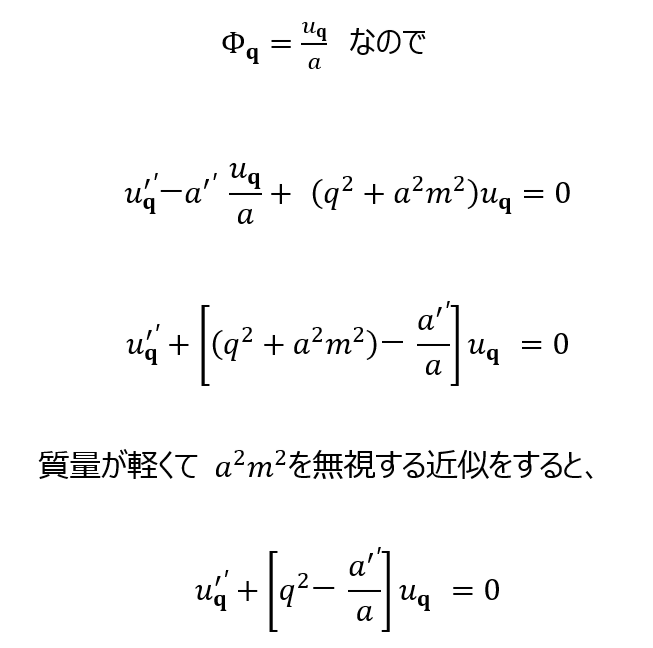
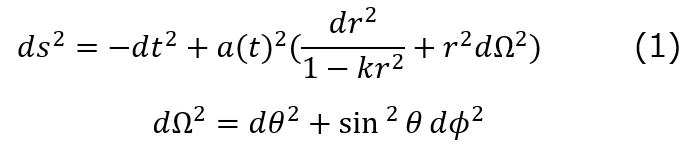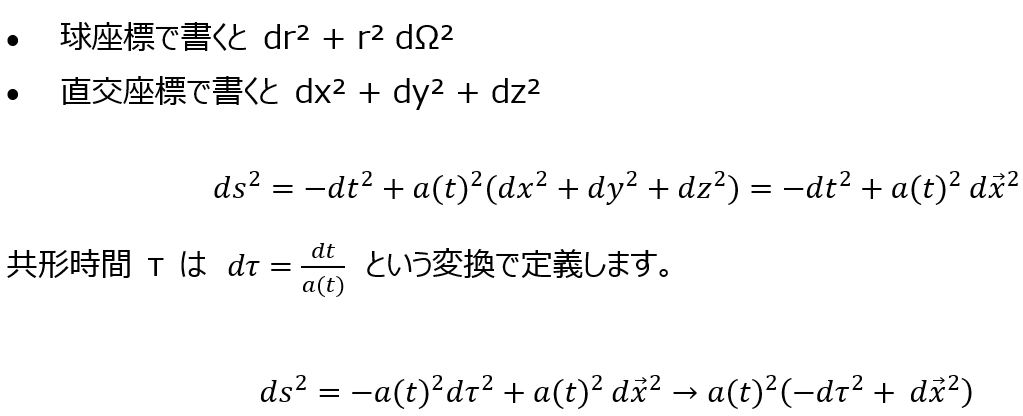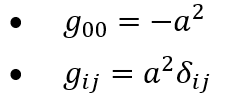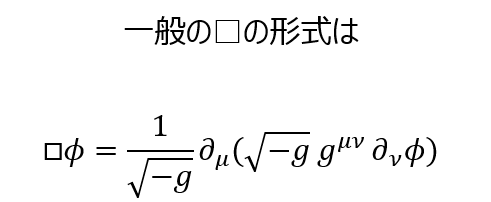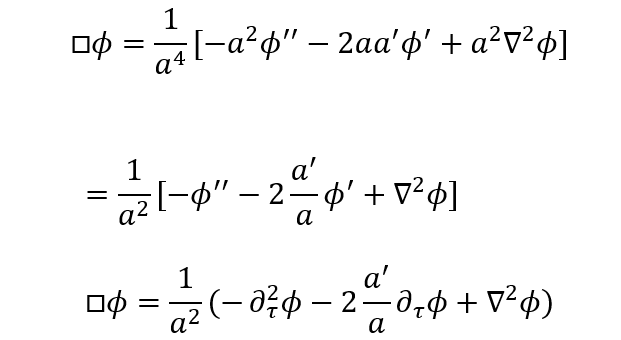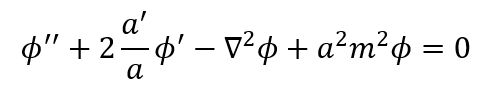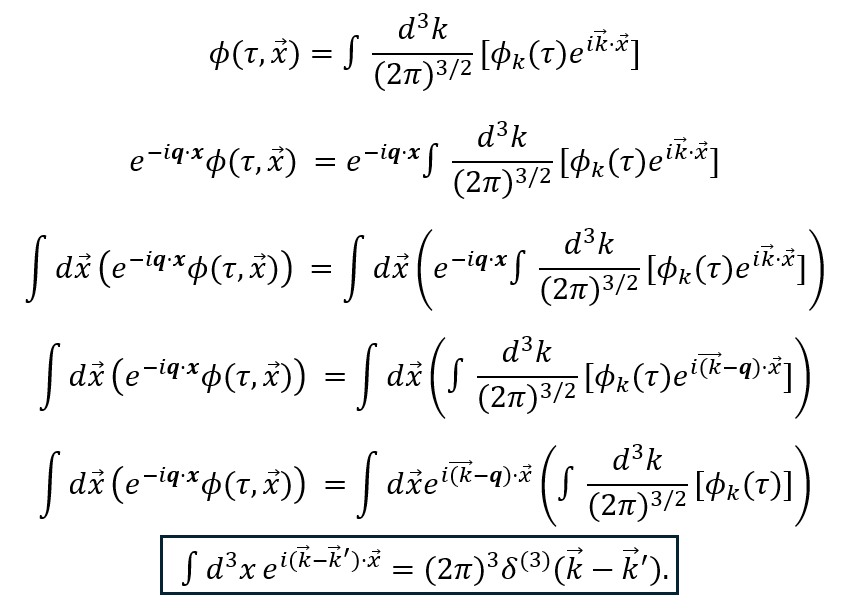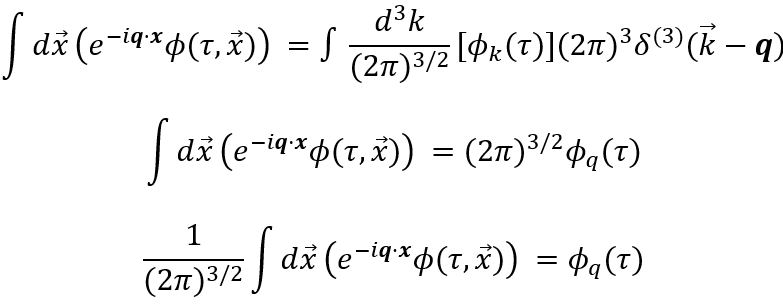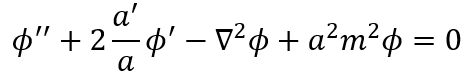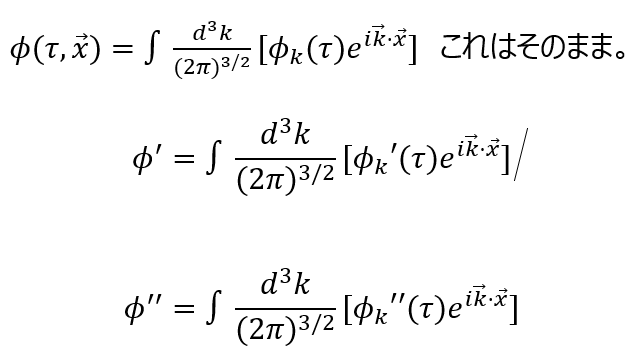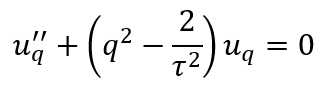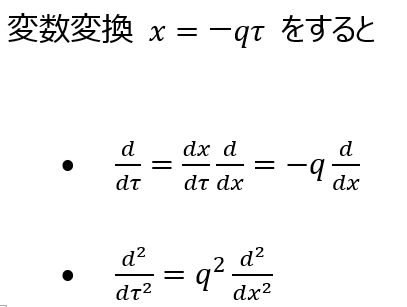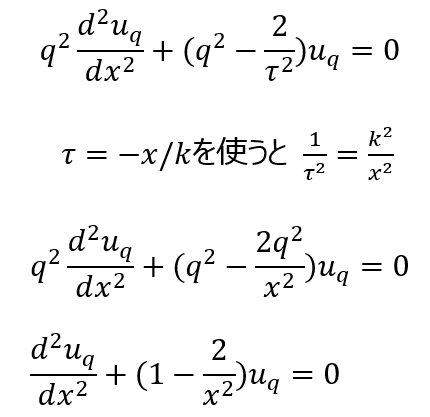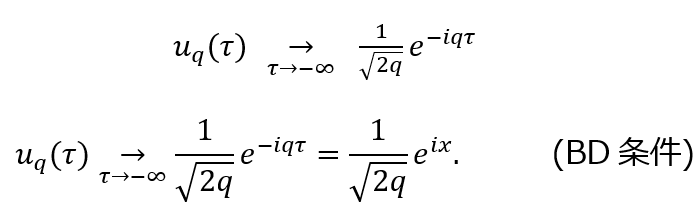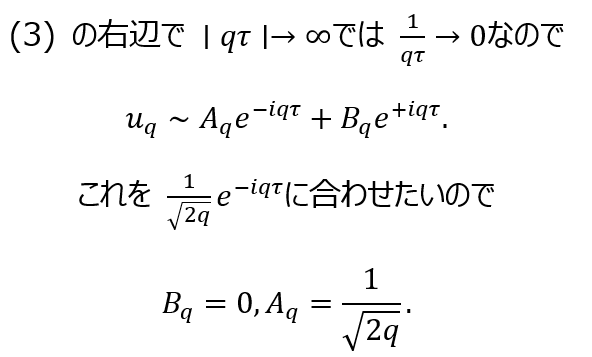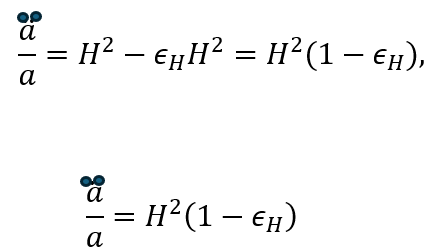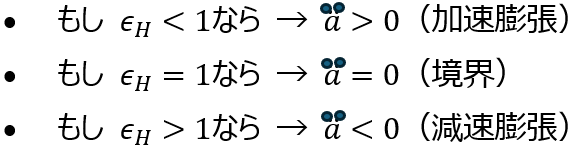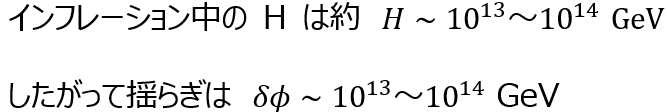奇妙な話だが1998年の超新星観測が「宇宙は加速している=Λ>0 必須」と示し、大発見になった。
宇宙の加速膨張の発見は、2011年のノーベル物理学賞として正式に表彰されました。
これは宇宙論の歴史でもトップクラスに重要な発見で、しばしば「宇宙論の革命」と呼ばれます。
しかし、これまでの勉強で既に宇宙の加速膨張は既知だったはずです。

どういうことなの?
実際は「物理学者は「Λ= 0」だと思っていた」という事らしいです。
まず、アインシュタインは「宇宙は静的」と信じていたため Λ を導入した。だが
(1)1929 年にハッブルの膨張発見により静的宇宙モデルは不要になった。
(2)そしてΛ には物理的根拠がなかった。
(3)ただの定数項を入れるだけで自由度を増やしてしまうため気持ち悪い。
(4)物質宇宙モデル(Λ=0)が観測とよく一致していた。
ということで物理学者は「Λ= 0」だろうと思って居たようです。逆に70 年間、宇宙はむしろ重力によって減速しているはずだと信じられていた。
ところが1998年にどのくらい減速しているのかの精密な観測結果、負の減速(つまり加速)を観測してしまい、初めて Λ>0 が観測的に必須になった←「加速膨張の大発見」。
数学的に Λ を入れられることは昔から分かっていたが、“実際の宇宙に Λ が本当に存在する”
ということを観測が初めて示したわけです。
インフレーションではインフラトン場によって加速膨張したので同じものでは?
と思ってしまうがインフレーションの終わりに熱に転換されてしまっているのでインフラトンの真空エネルギーは消えてしまっているはずです。
なのでΛ>0にしているものは謎です。これを引き起こすものをダークエネルギーと呼んでいます。
一方で、理論からΛを計算できるらしいです。その理論値は

現在のダークエネルギー密度の観測値は

ほぼ0に近い値です。つまり
「観測値がほぼ 0 なのに、理論は 10^120 を予測した → 120 桁大きい」
現代物理学最大の謎であり、宇宙論・量子場理論・重力理論のすべてが絡む最深部の問題らしい。
注)
古典的な再加熱・熱化理論 (たとえば Dissipative Effects on Reheating after Inflation) によると、熱化にはインフラトン decay → 放出粒子 + 散乱 + 相互作用など複合的な過程が絡むため、単純な「インフラトン真空エネルギー → すぐ熱化 → 普通物質」という流れが必ずしも保証されるわけではないようです。
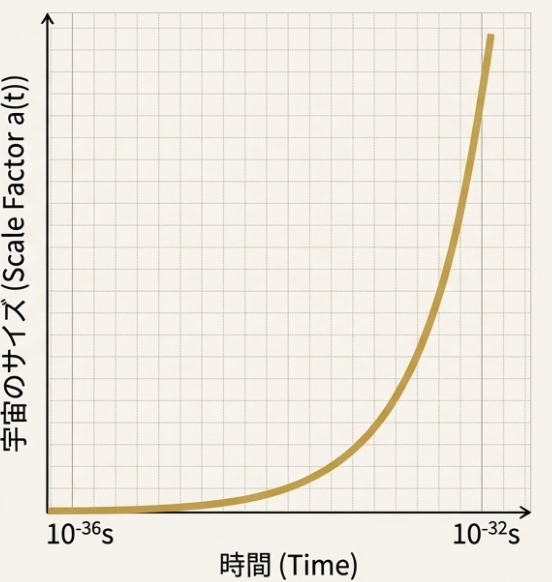
![]()
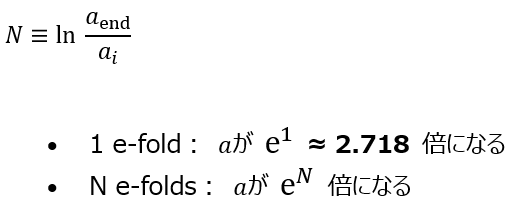
が自然に登場します。膨張率 から、所要時間 は
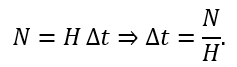
![]()
![]()
![]()
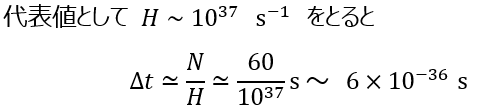
![]()