Note7 多様体上の接ベクトル場

ベクトル場はベクトルが多様体上の点の関数のようになっている。ベクトルではなくスカラーならスカラー場という事になる。イメージ的には各点にベクトルがくっ付いているような感じだ。

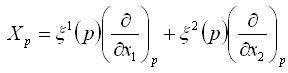
接ベクトル場は多様体の各点で定義されると考えると


として多様体M上の接ベクトルでM上の各点P上に対応して接ベクトルを考える事ができます。この写像をベクトル場という。定義からベクトル場は次のように書くことが出来る。

と定義することで各点に対応したベクトル場が定義されます。


各点に接ベクトルが付随したようなイメージになる。こうして各成分ζが多様体上の関数となります。そうすると各成分の微分を考える事ができて、各成分が微分可能なときにベクトル場Xpは微分可能と呼ばれます。
ベクトル場は各点に生えたベクトル全体だった。つまり各点pに対して、

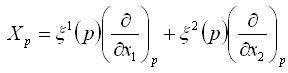
ここで異なるベクトル場Yを考えてみる。

互いに別のベクトル場だけど、

と約束してしまうとベクトル場そのものが一纏めにして再びベクトルとして蘇る事になる。つまり各点に生えたベクトル全体が一つのベクトルのように計算しても良い事になる。なかなか直感的で良い。

今日は「現代微分幾何入門 野水克己　著」p５でした。