こんな恐ろしい制限というか条件を満足するテンソルは知られていて、次式の定数倍が唯一らしい。

ただし、ビアンキの恒等式から
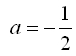
定数Λは一意に決まらないので0と置くと目的の一般共変な式は
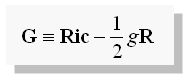
これをアインシュタイン・テンソル (Einstein tensor)と言います。
先程の全ての条件を全て満たした美しい式(テンソル)です。もちろん、

であるが、次のような共変(発散)微分がゼロとなるテンソルTとkを定数として
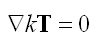
を使うと一つのアイデアとして次のように置く事ができます。
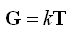
これは一般相対性理論における重力場方程式と殆ど同じ形になっている。と、ここまでは幾何学の話だけど、少しだけ物理との接点を参考までに見てみると、Tをエネルギー・運動量テンソルと呼ばれる量と考え、一般共変性をもつ重力場方程式として
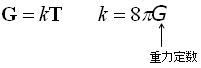
を仮定するのが一般相対性理論ということらしい。kは重力場が十分弱いときはニュートン力学のポアッソン(Poisson)方程式に一致しなければならないという仮定から決定された値のようです。もっともエネルギー・運動量テンソルの正体が今の私には良く分かっていないので何とも言えないですが、様々な実験、検証を経ていて現在この方程式を疑うような事例は見つかっていないようです。ところで通常は次のような局所表示が用いられるようです。
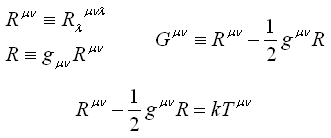
先程の事からもこの式はとても凄い性質を持っている。それは勝手な座標変換を行っても共変(形を変えない式)で共変(発散)微分がぴったりゼロになるという美しさ(凄い性質)を持っている。その背景にはリーマン幾何学におけるビアンキの恒等式という恒等的にゼロになる公式の存在が重要なのだろう。アインシュタインは「晩年に思う」でこう言っています。
「左辺は高級な大理石だが右辺は木材だ」
さらに
「これは微分幾何学の勝利である」とも。

ただし、ビアンキの恒等式から
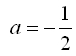
定数Λは一意に決まらないので0と置くと目的の一般共変な式は
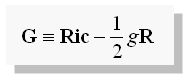
これをアインシュタイン・テンソル (Einstein tensor)と言います。
先程の全ての条件を全て満たした美しい式(テンソル)です。もちろん、

であるが、次のような共変(発散)微分がゼロとなるテンソルTとkを定数として
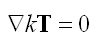
を使うと一つのアイデアとして次のように置く事ができます。
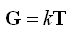
これは一般相対性理論における重力場方程式と殆ど同じ形になっている。と、ここまでは幾何学の話だけど、少しだけ物理との接点を参考までに見てみると、Tをエネルギー・運動量テンソルと呼ばれる量と考え、一般共変性をもつ重力場方程式として
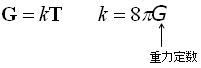
を仮定するのが一般相対性理論ということらしい。kは重力場が十分弱いときはニュートン力学のポアッソン(Poisson)方程式に一致しなければならないという仮定から決定された値のようです。もっともエネルギー・運動量テンソルの正体が今の私には良く分かっていないので何とも言えないですが、様々な実験、検証を経ていて現在この方程式を疑うような事例は見つかっていないようです。ところで通常は次のような局所表示が用いられるようです。
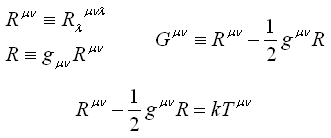
先程の事からもこの式はとても凄い性質を持っている。それは勝手な座標変換を行っても共変(形を変えない式)で共変(発散)微分がぴったりゼロになるという美しさ(凄い性質)を持っている。その背景にはリーマン幾何学におけるビアンキの恒等式という恒等的にゼロになる公式の存在が重要なのだろう。アインシュタインは「晩年に思う」でこう言っています。
「左辺は高級な大理石だが右辺は木材だ」
さらに
「これは微分幾何学の勝利である」とも。
(私のようなシロートに今日の数学的な行間は当分手が出ない禁断の地だろうと思った)。
「現代微分幾何入門 野水克己 著」p173を少しだけ。