Fは4元ベクトルポテンシャルに任意性が生じます。それは任意の時空の関数ζを使って
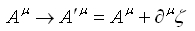
と変換しても変わりません。これは
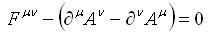
から明らかです。この変換を「ゲージ変換」と呼びます。とっても重要な概念のようです。
さらに、このゲージ変換の任意性をうまく使うと良い事があるという事らしい。その選び方は次を満たす関数としてみる。
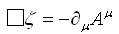
なんとも都合の良い選び方だと言う事が
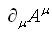
をゲージ変換してみると分かる。
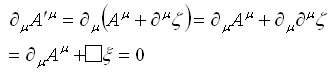
つまり、このゲージ変換でわかるように任意だったζをこの例のように固定してやると最初から
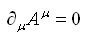
とされた事になるので電磁場の式はさらに綺麗になって、
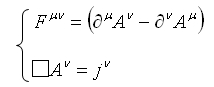
となる。なんとも作為的な気がしないでも無いがこの任意性のお陰で簡単な式にまとまった訳だ。ともかくこのようなゲージ条件をローレンツゲージ条件と呼び色んなところで顔を出します。
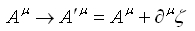
と変換しても変わりません。これは
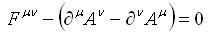
から明らかです。この変換を「ゲージ変換」と呼びます。とっても重要な概念のようです。
さらに、このゲージ変換の任意性をうまく使うと良い事があるという事らしい。その選び方は次を満たす関数としてみる。
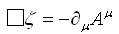
なんとも都合の良い選び方だと言う事が
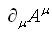
をゲージ変換してみると分かる。
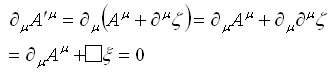
つまり、このゲージ変換でわかるように任意だったζをこの例のように固定してやると最初から
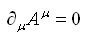
とされた事になるので電磁場の式はさらに綺麗になって、
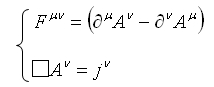
となる。なんとも作為的な気がしないでも無いがこの任意性のお陰で簡単な式にまとまった訳だ。ともかくこのようなゲージ条件をローレンツゲージ条件と呼び色んなところで顔を出します。
余談(失敗談)
記号と単位系をうまく使うことで計算の見通しがよくなる点をあらためて痛感(体感)しました。今回の計算であっさりと確認できた関係
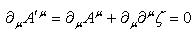
は通常行われる電磁気学の方法で計算していたら大変な事になっていました。例えば同じ計算は、こんな感じです。
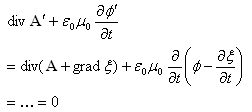
(その道の人以外は)見た目で嫌に成りますね。
電磁気といえばdivもgradもcurlがやたら出てきて嫌になった方も多いと思います。一切divもgradもcurlも使ってない!! 恐るべし記述方法の選択!!
記号と単位系をうまく使うことで計算の見通しがよくなる点をあらためて痛感(体感)しました。今回の計算であっさりと確認できた関係
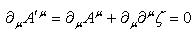
は通常行われる電磁気学の方法で計算していたら大変な事になっていました。例えば同じ計算は、こんな感じです。
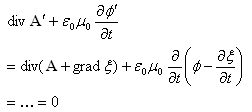
(その道の人以外は)見た目で嫌に成りますね。
電磁気といえばdivもgradもcurlがやたら出てきて嫌になった方も多いと思います。一切divもgradもcurlも使ってない!! 恐るべし記述方法の選択!!
それと情け無い話をひとつ。

