Note8 多様体上の接ベクトルと微分（１）

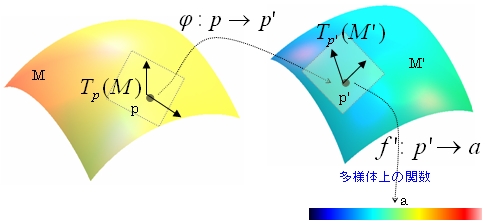
多様体Mから多様体M'への微分可能な写像

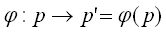
で次のような線形写像、（Tｐ(M)はM上の点ｐの接ベクトル全体の集合）

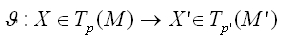
つまり、

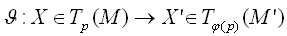
をφのｐにおける微分というらしい。なんで微分なのか？ともかくそのような線形写像を

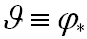
と書きます。つまり、線形写像

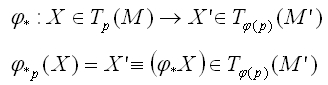
を次のような計算とする。

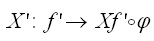
つまり、

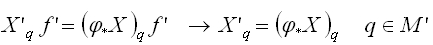
で、これが微分と言われてもイメージが、、、かなり直感的な理解がしづらい。そこで局所座標系をつかって生で見てみよう。ｐの局所座標系をｘとして接ベクトルは次のように書けるはずです。

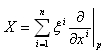
また、ｐ’つまりφ(p)の局所座標系をyとすと、

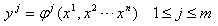
と書けるはずです。

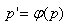
とp'の局所座標は

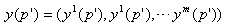
なのでp'の局所座標は次のように書くことが出来ます。

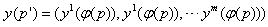
なので、

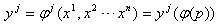
です。

そうすると

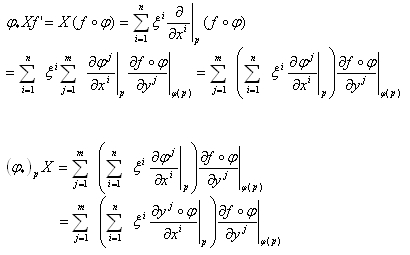
ですから、

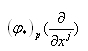
はφ(p)の局所座標系yでそこの基底の一次結合になっているわけで、具体的には、

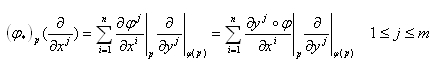
という線形写像になっているという訳ですね。

これを行列で書いてみると

ちょうどJacobi（ヤコビ）行列になっている事が分かります。n=mの場合は正方行列になるので行列式

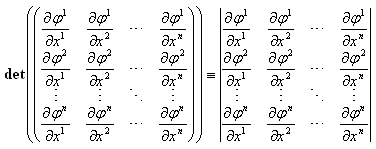
が定義できます。これはJacobian(ヤコビアン)になっています。なのでなんとなく写像の微分というイメージが湧きますが、まだ、微分というイメージが湧かないですね。

次回はこのイメージをすっきりさせたいと思います。

今日は「現代微分幾何入門 野水克己　著」p６を解体してみた。