今日は

という関係をもう少し抽象化してみて見たいと思います。
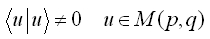
とする時
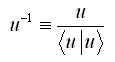
と定義するとこれは逆元になっています。
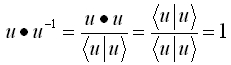
同様に
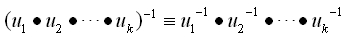
と考えれば良い。つまりクリフォード積による群になっているようです。ここでディラックス・ピノールの変換と関係する次の関係を思い出しますと
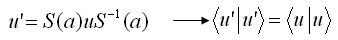
https://cat-falcon.hatenablog.com/entry/25368139
この変換式と同じ形式のクリフォード積による変換
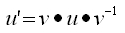
を考えてみると
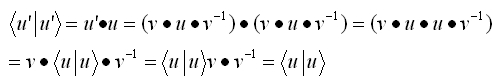
という事で全く同じ挙動を示しています。それで
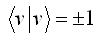
だけを考えていても一般性を失う事は無い、ということで
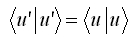
を満たす変換
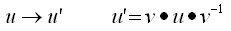
が構成できます。

という関係をもう少し抽象化してみて見たいと思います。
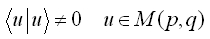
とする時
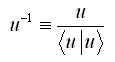
と定義するとこれは逆元になっています。
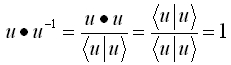
同様に
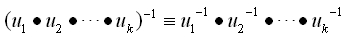
と考えれば良い。つまりクリフォード積による群になっているようです。ここでディラックス・ピノールの変換と関係する次の関係を思い出しますと
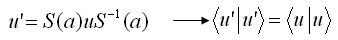
https://cat-falcon.hatenablog.com/entry/25368139
この変換式と同じ形式のクリフォード積による変換
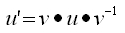
を考えてみると
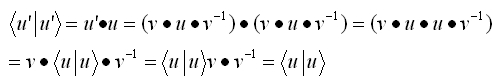
という事で全く同じ挙動を示しています。それで
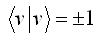
だけを考えていても一般性を失う事は無い、ということで
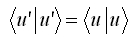
を満たす変換
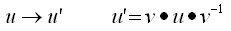
が構成できます。
えーっと、まだ調べが付いていないので何とも言えないのだけどクリフォード積による群を作るとその群の表現という意味で行列に結びつきます。そうするとそんな表現の一種がスピノールという概念に繋がっているのでは無いかと推測しているのですがどうなんでしょうかね。