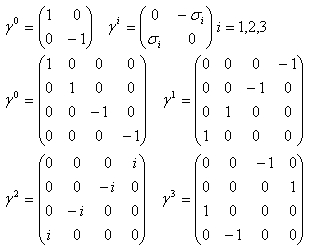Note103 ディラック・ガンマと次元について

もうしばらくスピノル（スピノール）を見てみようと思う。
これまででパウリ行列とディラック・ガンマ行列の具体的な形を覚えました。
https://cat-falcon.hatenablog.com/entry/13660821

パウリ行列

ディラック・ガンマ行列

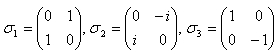
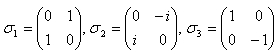
しかし、これは一つの具体的な形で、これで無ければならないといものでも無く

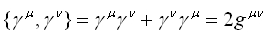
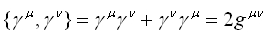
を満たしているような行列であれば良い。
https://cat-falcon.hatenablog.com/entry/14171942。

一般に、関係式

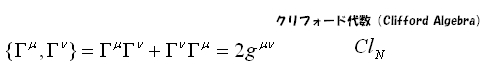
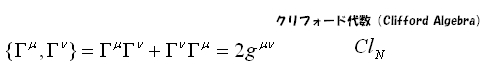
を満たすような代数をクリフォード代数（Clifford Algebra）というらしい。Nは次元。

なのでディラック方程式に出てくるγがN = 4 という事になる。

そこで素朴な疑問が生じる。

ベクトルやテンソルは何次元でも良かった。
基本的な原理や数学的というかそういった制約から３とか４という次元の量になっているような事は無かった。多次元の運動方程式は記述しようと思えば出来る。だけどディラックガンマは最初から４次元になっている。もっと他の次元のディラックガンマを構成できるんだろうか？と。

「クリフォード代数」とか「スピン群」とかいう物がその背景にあるようだ、、、

まあ、そんな高度な事は今の私にはどうでもいいのです。