先日までの話を一般化したものが多様体と呼ばれるものになります。
少し、今までのイメージを抽象化して描くと
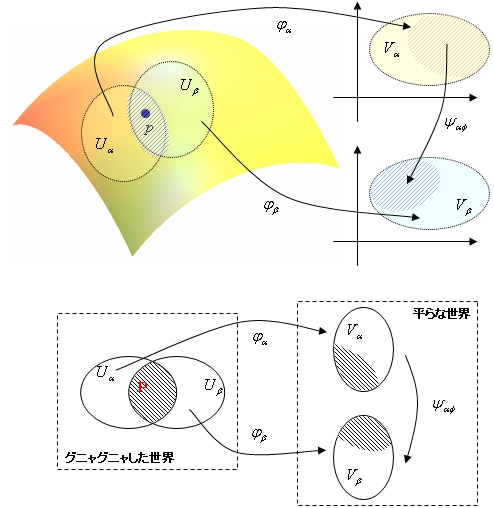
そんな訳で数学ではこんな図が描かれるって言う事ですね。多様体でも特に重要なのは座標変換Ψαβが微分可能な関数であるような微分可能多様体と呼ばれるもので、物理では多様体と言えば通常は微分可能多様体を指します。また、球の場合は2次元でしたが一般にはn次元を対象にします。
なのでUV座標系という記述は2次元だけなのでn次元の場合
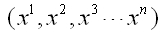
という記述で座標系を表記します。多様体上の点をpとするときその局所座標は各点p毎に異なるわけですから、点pの局所座標は関数関係にあるので、
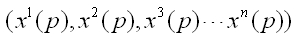
と書くことが出来ます。それで、微分可能と言えるには、
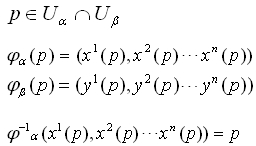
なので、座標変換は
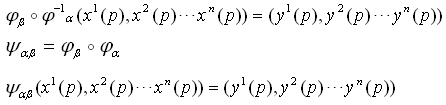
なのでn個の関数が全て微分可能なときです。

もう少し書いておくと
全ての点pに対して局所座標と近傍Uのセット(これを座標近傍と言う)で多様体Mは
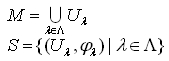
と書ける。Sが地図帳ですね。だから全ての地図の上でn個の座標変換関数が全て微分可能な時という事になります。
少し、今までのイメージを抽象化して描くと

そんな訳で数学ではこんな図が描かれるって言う事ですね。多様体でも特に重要なのは座標変換Ψαβが微分可能な関数であるような微分可能多様体と呼ばれるもので、物理では多様体と言えば通常は微分可能多様体を指します。また、球の場合は2次元でしたが一般にはn次元を対象にします。
なのでUV座標系という記述は2次元だけなのでn次元の場合
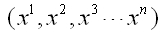
という記述で座標系を表記します。多様体上の点をpとするときその局所座標は各点p毎に異なるわけですから、点pの局所座標は関数関係にあるので、
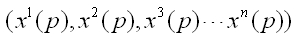
と書くことが出来ます。それで、微分可能と言えるには、
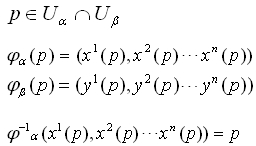
なので、座標変換は
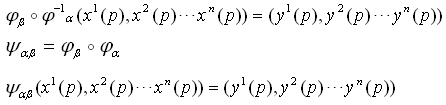
なのでn個の関数が全て微分可能なときです。

もう少し書いておくと
全ての点pに対して局所座標と近傍Uのセット(これを座標近傍と言う)で多様体Mは
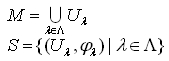
と書ける。Sが地図帳ですね。だから全ての地図の上でn個の座標変換関数が全て微分可能な時という事になります。
結局のところ多様体は複雑なグニャグニャした世界を理解するための概念でそれを平坦な地図をたくさん作って地図帳にまとめて理解する。というようなイメージなんだろうと思います。
※あくまで直感的な定義なので正確な定義は数学の本を見てくださいね。

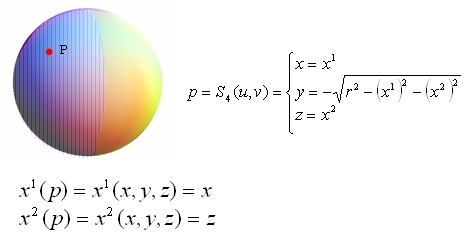
なので局所座標は(x,z)という事になります。この局所座標系の元では(x,z)は球面上の点pを表す事になります。

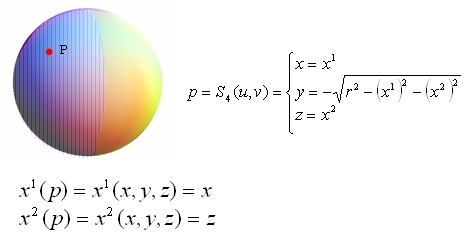
なので局所座標は(x,z)という事になります。この局所座標系の元では(x,z)は球面上の点pを表す事になります。
このように考えると多様体上の点pは局所座標系を背景にその局所座標と同一視する事も出来ますから意味的に局所座標系を背景として考えているのであれば
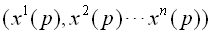
を単にpと書いても誤解は生じませんね。こういう略記は殆ど断り無く行われます。
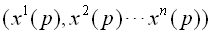
を単にpと書いても誤解は生じませんね。こういう略記は殆ど断り無く行われます。
今日は「現代微分幾何入門 野水克己 著」p2でした。