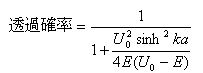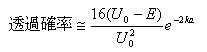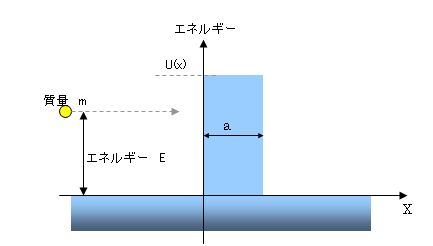
ここでE < U(x) である必要は無い。
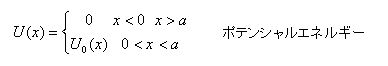
A,B,C,F,G はゼロで無い係数とするとき波動関数Ψは次のような形になる。
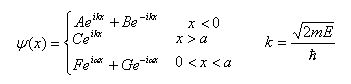

この解から粒子の存在位置の観測で壁の中における存在確率がゼロになっていない事がわかる。さらに解は
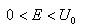
の場合(壁をジャンプして乗り越える事が出来ない状況)でも壁の外にも観測される可能性を示してる。
これを「トンネル効果」と呼ぶ。さらに興味深いのは
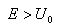
の場合(ジャンプして壁を乗り越える場合)でも乗り越えられない場合がある事を示している。ここで注意したいのは「ジャンプして壁を乗り越える」エネルギーを持っていても乗り越えられないという事を示している訳ではないという点である。例えて言えば5mのジャンプが出来る選手が4.5mに届かず5mが飛べなかったケースという意味ではなく、5mの高さでジャンプしているにも関わらず4.5mの壁が乗り越えられないような状況である。
|Ψ|^2 のイメージ
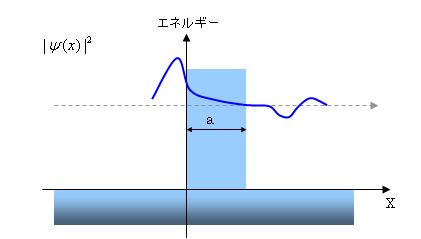
粒子がこの|Ψ|^2という曲線に沿って動いている訳ではない。|Ψ|^2の曲線はあるX座標で観測を行ったときにそこで粒子の存在が認められる「確率」でしかない。従って観測ごとに粒子は位置を微妙に変化させて観測されるという事になる。粒子は観測していないときは波の性質があるため質点として粒子が観測されるのは観測した時だけである。なので比喩的に表現すれば粒子は壁の中をすり抜けてくるというよりあるとき突然壁の向こう側に出現するといった方が的を得ているかも知れない。もっともある間隔でじわじわと壁をすり抜けてくるような状況が無いとは否定は出来ないだろが不確定性原理によって連続的な粒子の移動(座標と運動量)はある一定の揺らぎの範囲でしか観測できない。

粒子がこの|Ψ|^2という曲線に沿って動いている訳ではない。|Ψ|^2の曲線はあるX座標で観測を行ったときにそこで粒子の存在が認められる「確率」でしかない。従って観測ごとに粒子は位置を微妙に変化させて観測されるという事になる。粒子は観測していないときは波の性質があるため質点として粒子が観測されるのは観測した時だけである。なので比喩的に表現すれば粒子は壁の中をすり抜けてくるというよりあるとき突然壁の向こう側に出現するといった方が的を得ているかも知れない。もっともある間隔でじわじわと壁をすり抜けてくるような状況が無いとは否定は出来ないだろが不確定性原理によって連続的な粒子の移動(座標と運動量)はある一定の揺らぎの範囲でしか観測できない。
さらに言えば(もっとおざっぱに言えば)
壁をすり抜けてしまう確率は
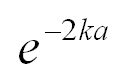
として見積もる事が出来る。
ディラック定数1.05457148 × 10^-34の逆数9.48× 10^33が大きく効いているため日常的な値として質量を1g等という値を打ち込もうなら電卓はおろかMathematicaでもギブアップするほど小さな値の確率となる。なので尋常な値は計算できない。
さて誰しも(?)(当然そういった考えも浮かぶだろう)次のような問題を考えたくなる。
●10mの高さの壁を60kgf の体重の人間がこの壁の向こうに抜ける確率



壁をすり抜けてしまう確率は
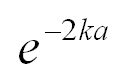
として見積もる事が出来る。
ディラック定数1.05457148 × 10^-34の逆数9.48× 10^33が大きく効いているため日常的な値として質量を1g等という値を打ち込もうなら電卓はおろかMathematicaでもギブアップするほど小さな値の確率となる。なので尋常な値は計算できない。
さて誰しも(?)(当然そういった考えも浮かぶだろう)次のような問題を考えたくなる。



はおよそ

ここに並ぶゼロの数は10の24乗個である。このゼロの列は1cmの枠に3個づつ並べて書いたとして数十万光年の方まで続いてその先に1が出てくるような超超超超微小な値である。
| 0.00000000000000000000000000000000000...001% |

ここに並ぶゼロの数は10の24乗個である。このゼロの列は1cmの枠に3個づつ並べて書いたとして数十万光年の方まで続いてその先に1が出てくるような超超超超微小な値である。