Note11 ベクトル場との流れに沿った微分

今日は公式を一個だけ。

ベクトル場Xが生成する局所的な１助変数変換群をφt、ベクトル場Yが生成する局所的な１助変数変換群をψsとするとき、φtに沿って動いたベクトル場Yの変化は、


となりますね。この時流れが極微小な時（t が０に近いとき）はどうでしょうか？もう少し言い換えると変化率はどうでしょう？つまり、

少し、形式的な計算をして具体的な形を見てみましょう。

ベクトル場はM上の関数ｆに作用するのでしたからもう少し正確に書けば、

まず、複雑な表現になっている部分から計算してみますと多様体上の接ベクトルと微分（２）の

から、

なので、

ここで、次のように定義しておきます。

つまり、

これを代入すると、


と、なりますから

この結果から、

という美しい関係が出てきます。こんなところにも交換関係が出てくるのですね。
http://blogs.yahoo.co.jp/cat_falcon/6395431.html
http://blogs.yahoo.co.jp/cat_falcon/12045917.html
http://blogs.yahoo.co.jp/cat_falcon/14476613.html
http://blogs.yahoo.co.jp/cat_falcon/14518433.html
http://blogs.yahoo.co.jp/cat_falcon/14561694.html
http://blogs.yahoo.co.jp/cat_falcon/14685807.html

実はこれがLie微分（リー微分）と呼ばれるものになっていました。

今日は「現代微分幾何入門 野水克己　著」p12。

ただ「この事実が知られている」とあっさり。多少は導出について書いて欲しかった。

ここで、

と定義されM上の点pの接ベクトルとなる。

括弧積の局所表示を使って確かめてみる。括弧積の局所表示次のようになる。




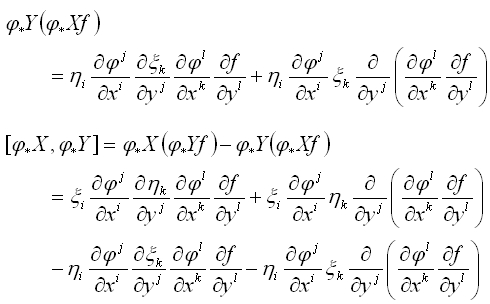
※途中から総和（Σ）を省略した。

※正確（数学的）なことに関しては専門書を見てくださいね。