質量の部分が処理の悪さを引き起こしていそうなのでもう少し整理して

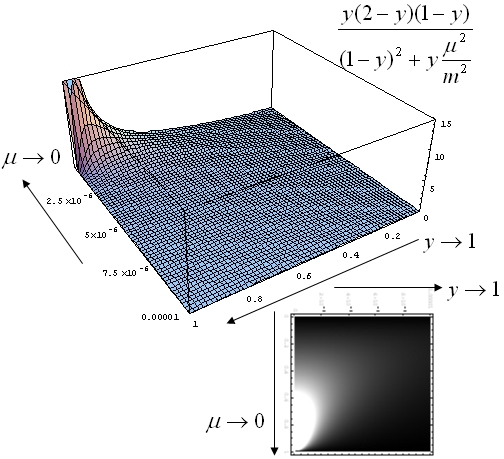


さて、ここでも思考停止。どうしたものか、、、結局、
ここで発散を切断するのが常套のようだ。(※1) ここで被積分関数を
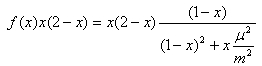
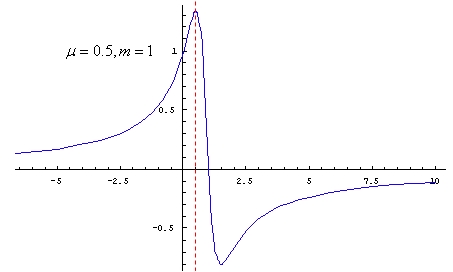
として積分をこの関数の極大値で切断(cutt-off)してやります。まず、この関数のグラフを見てみます。

極大となる位置は次式をxについて解けば良いから
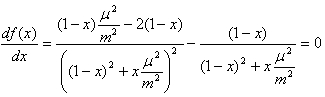
解は次のようになります。
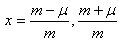
またグラフから明らかなように極大となるのは
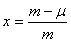
です。従って切断した積分は

もとの式を思い出すと
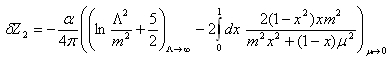
だったから
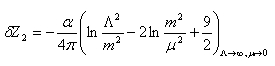
どうなんだろうか?
ここで発散を切断するのが常套のようだ。(※1) ここで被積分関数を
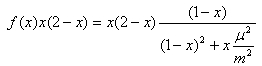
として積分をこの関数の極大値で切断(cutt-off)してやります。まず、この関数のグラフを見てみます。


極大となる位置は次式をxについて解けば良いから
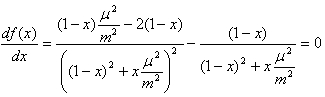
解は次のようになります。
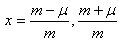
またグラフから明らかなように極大となるのは
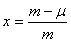
です。従って切断した積分は

もとの式を思い出すと
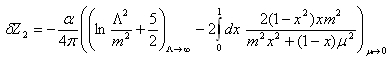
だったから
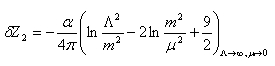
どうなんだろうか?