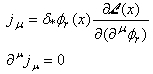今日はネーターカレント(Noether current)を実際に導出してみようと思います。
「場の解析力学」高橋康・著p100~p102のやり方の説明はちょっとピンと来なかったので途中から別のやり方でやってみた(がやり終わってからそう言う事かとわかった)。
「場の解析力学」高橋康・著p100~p102のやり方の説明はちょっとピンと来なかったので途中から別のやり方でやってみた(がやり終わってからそう言う事かとわかった)。
それで無限小変換
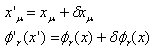
これにともなうラグランジアン密度の変化

無限小変換で最小作用の原理より作用の変分(作用積分の違い)は
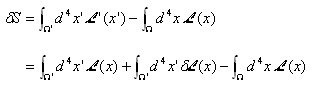
変数変換のヤコビアンは無限小変換だから簡単になって
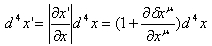
これを代入すると、

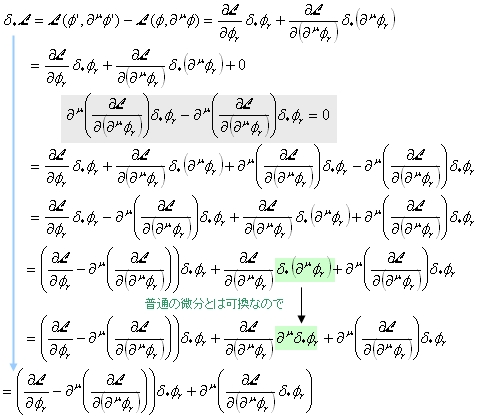
これから、
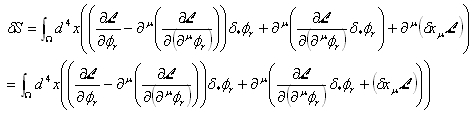
これから次のネーターの恒等式を得ます。
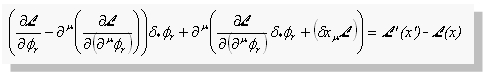
ここで不変性(対称性(symmetry))
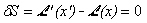
を仮定し、ハミルトンの原理から1項目はオイラー・ラグランジュ方程式なのでゼロとなりますから、結局次の結果を得ます。
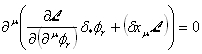
それで、
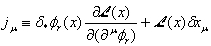
と定義すると、これがネーターカレント(Noether current)で直ぐ上の式から
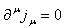
を満たすのは定義から明らかです。個人的には久しぶりにこれは美しい定理だと思った。
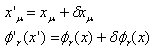
これにともなうラグランジアン密度の変化

無限小変換で最小作用の原理より作用の変分(作用積分の違い)は
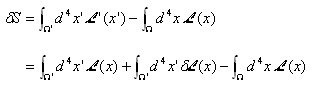
変数変換のヤコビアンは無限小変換だから簡単になって
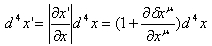
これを代入すると、

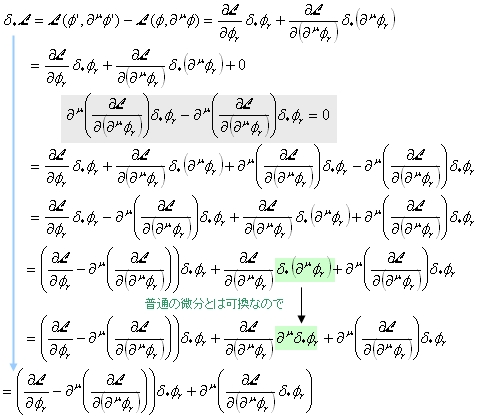
これから、
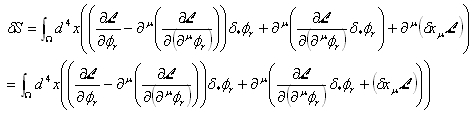
これから次のネーターの恒等式を得ます。
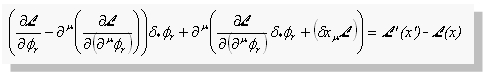
ここで不変性(対称性(symmetry))
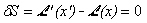
を仮定し、ハミルトンの原理から1項目はオイラー・ラグランジュ方程式なのでゼロとなりますから、結局次の結果を得ます。
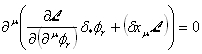
それで、
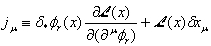
と定義すると、これがネーターカレント(Noether current)で直ぐ上の式から
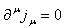
を満たすのは定義から明らかです。個人的には久しぶりにこれは美しい定理だと思った。
変換が体積を変えないような変換の場合は
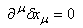
なので
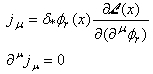
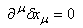
なので